Arquímedes y la corona del rei

Arquímedes y la corona del rei

Hieron II, rei de Siracusa, entregó-y a un orfebre un lingote d’oru puro pa que ficiera con él una corona (figura 1). Al recibir la corona yá fecha, al rei entró-y la sospecha de que l’orfebre hubiere cambiao parte del oru por otru metal; poro, pidió-y a Arquímedes, el sabiu más eminente del reinu, que lu sacara de duldes.

Figura 1. L’orfebre fizo una corona pal rei con un bloque d’oru puro

Arquímedes

Arquímedes nació en Siracusa nel añu 287 a. de C. y morrió na mesma ciudá nel añu 212 a. de C. Foi unu de los científicos más importantes de l’Antigüedá. Nel campu la Física estudió’l comportamientu los fluyíos en reposu. Inventó un torniellu pa bombiar agua y xubir granos, tierra y otres sustancies de granu finu, inventu que tovía s’utiliza güei sin munches variaciones. Otros inventos foron el polipastu, que ye un conxuntu de polees col que foi capaz de xubir un barcu con una sola mano. Nel campu les matemátiques calculó con muncha precisión el númberu pi, y inventó un procedimientu pa calcular árees precursor del cálculu integral d’anguaño.

Los metales de l'Antigüedá

Na época na que vivió Arquímedes solo se conocíen siete metales: estañu, fierro, cobre, plata, plomu, mercuriu y oru.

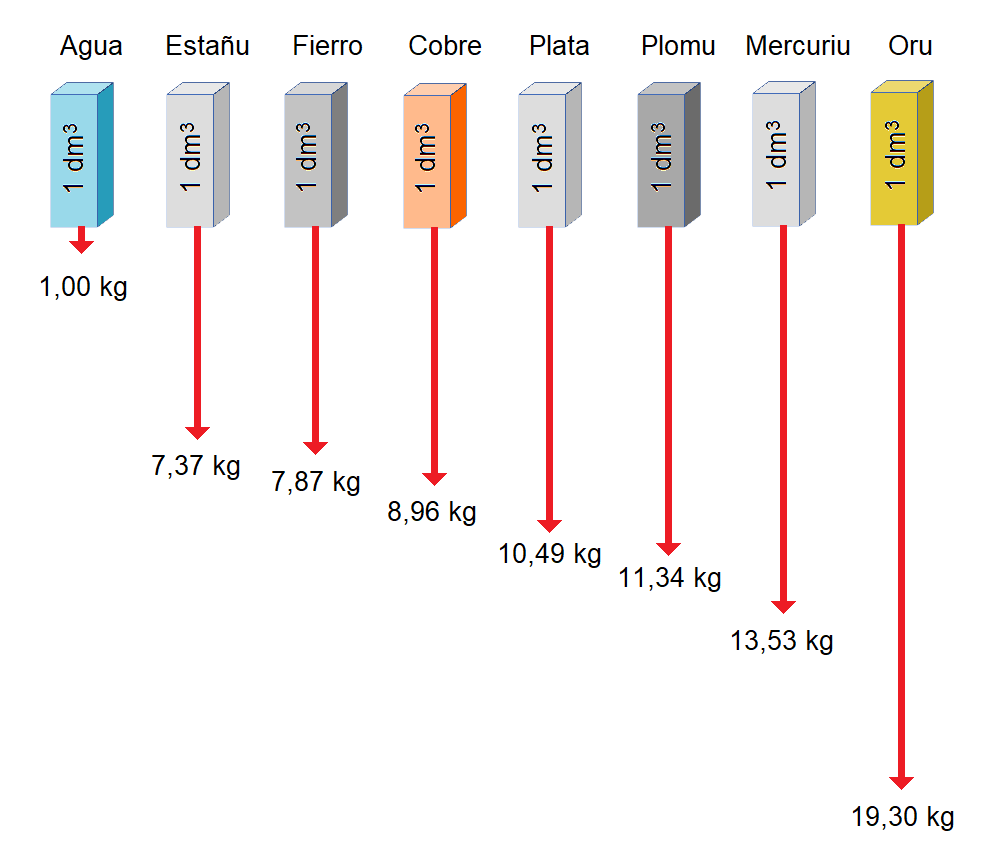
Na figura 2 tan representaos varios bloques iguales de 1 dm3 de volume. Los bloques tan fechos colos siete metales de l’Antigüedá. Hai tamién un primer bloque d’agua que, al ser ésta una sustancia conocida por toos, va permitinos comparar el so pesu col de los metales; ye sabío que 1 llitru d’agua ocupa 1 dm3 y pesa cuasi 1 kg (dicimos ‘cuasi’ porque en realidá 1 llitru d’agua pesa 0,999975 kg). Les fleches coloraes representen los pesos de los bloques.

Na figura 2 vemos que, por exemplu, un bloque macizu d’estañu de 1 dm3 pesa 7,37 kg, unu de fierro del mesmu tamañu pesa 7,87 kg y unu d’oru pesa 19,32 kg.

Na figura 3, a la izquierda del too, represéntase otra vez el bloque de 1 dm3 d’agua. A la derecha tan representaos bloques de los siete metales de l’Antigüedá. El volume de cada unu d’estos bloques ye’l que se correspuende col pesu de 1 kg. Por exemplu, 1 dm3 d’agua pesa 1 kg, lo mesmo qu’un bloque d’estañu de 0,14 dm3 y unu d’oru de 0,05 dm3.

De la figura 2 despréndese que l’oru yera’l metal más pesáu de l’Antigüedá. De la figura 3 despréndese que si se quería tener un pesu determináu de metal, l’oru yera’l metal que menos volume ocupaba de los conocíos n’Antigüedá.

El problema la corona del rei

Arquímedes tenía ante sí una corona que pesaba lo mesmo que’l lingote usáu pa facela. Si l’orfebre hubiere obrao correutamente, el volume de la corona tendría que ser tamién el mesmu que’l del lingote (figura 4-a). Pero si l’orfebre hubiere cambiao parte del oru por otru metal, el volume de la corona tendría que ser mayor que’l del lingote d’oru puro (figura 4-b).

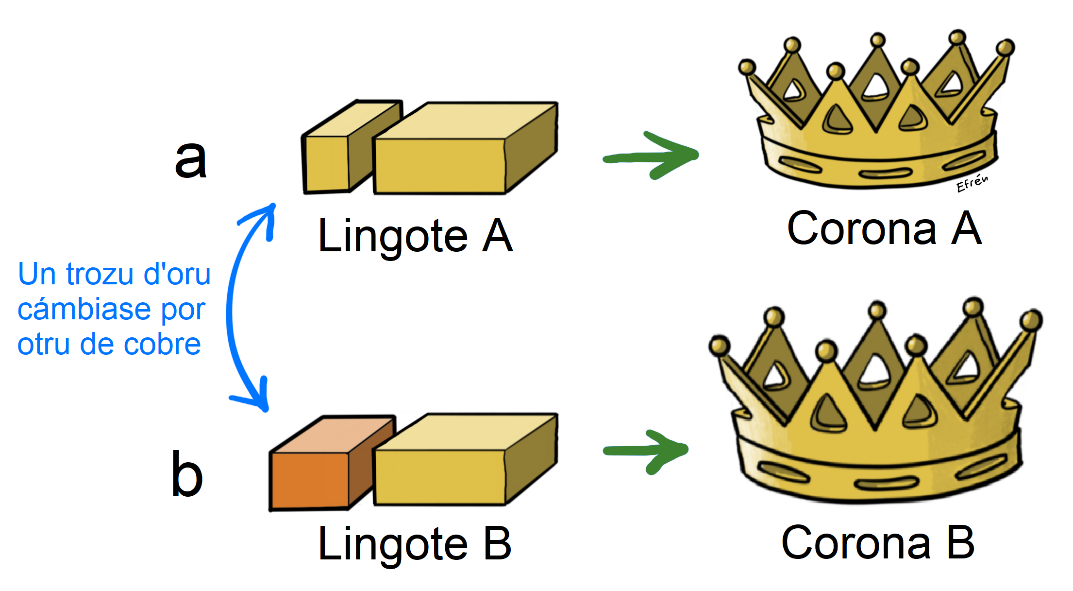
Figura 4. El volume ocupáu pola corona B ye mayor que’l volume del lingote A.

El problema yera fácil de resolver en teoría, pero na práctica tenía una dificultá importante, ¿cómo se podía conocer el volume de la corona? La so forma irregular facía mui complicáu el cálculu usando procedimientos xeométricos; y nun yera plan de fundila pa convertila nun bloque que se pudiera midir con facilidá.

Con esti problema na cabeza Arquímedes foi a dase un bañu; al metese na bañera dióse cuenta que’l nivel del agua xubía hasta cuasi esbarbase de la bañera; yera como si l’agua aumentase de volume. Salió del agua y el nivel baxó. Volvió a metese y el nivel volvió a xubir. Arquímedes pensó que, si l’agua nun se comprimía nin s’expandía, l’aumentu aparente del volume del agua tenía que ser igual que’l volume qu’ocupaba el so cuerpu. Acababa de descubrir una forma de medir el volume de la corona ensin tener que fundila.

El volume d'un cuerpu somorguiáu nun líquidu ye igual al volume del líquidu desplazáu.

Cuenten qu’Arquímedes, emocionáu col descubrimientu, salió pa la calle desnudu gritando ¡eureka!, que ye una palabra griega que quier dicir “alcontrélo”.

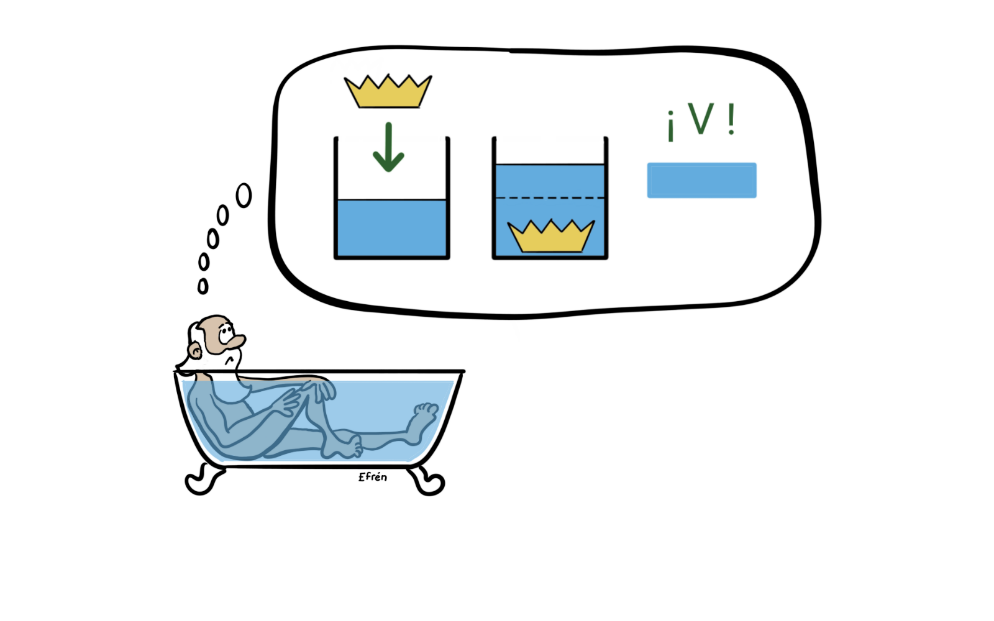
Figura 5. L’aumentu aparente del volume del agua ye igual al volume ocupáu pola corona.

Gracies a esti descubrimientu Arquímedes pudo saber si’l volume de la corona se correspondía col so pesu d’oru puro. De toes maneres, hai quien piensa que colos medios qu’había n’aquella dómina nun se podía tener una precisión aceptable pa resolver el problema, pero qu’Arquímedes pudo resolvelu sin necesidá de conocer el volume de la corona. El procedimientu pudo ser el que se cuenta de seguío.

El principiu d'Arquímedes

Toos podemos esperimentar la sensación de perder pesu cuando nos metemos dientro l’agua, por exemplu na piscina o na mar. Pola mesma razón, al llevantar un oxetu pesáu dientro l’agua paeznos más llixeru que fuera d’ella. Arquímedes conocía esti fenómenu y foi’l primeru en llegar a la conclusión de que’l pesu que pierde un cuerpu somorguiáu nun líquidu ye igual al pesu del agua desplazao pol cuerpu, lo que lu llevó a enunciar el siguiente principiu.

"Un cuerpu somorguiáu nun líquidu esperimenta un empuxamientu p'arriba igual al pesu del líquidu desplazáu pol cuerpu".

La figura 6 representa un cuerpu somorguiáu nun líquidu dientro un recipiente. El cuerpu recibe l’aición de dos fuercies verticales y de sentíu contrariu: una ye’l so pesu (P) que tira d’él p’abaxo y la otra ye l’empuxamientu (E) que tira d’él p’arriba. Esi empuxamientu p’arriba ye igual y de sen contrariu al pesu del líquidu desplazáu pol cuerpu.

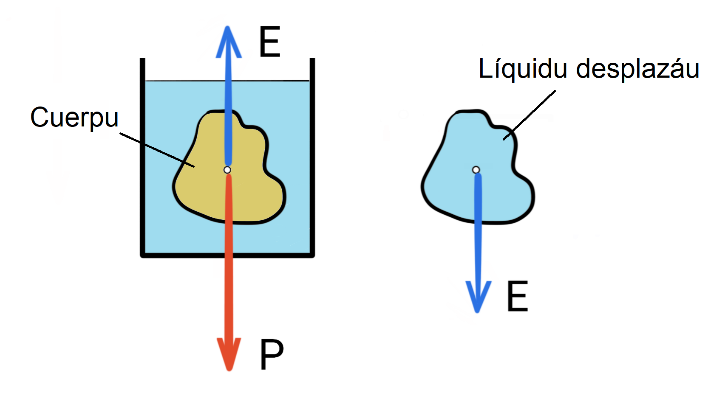
Figura 6. Principiu d'Arquímedes

A vueltes col problema la corona del rei

Teniendo en cuenta esti principiu, ye mui posible qu’Arquímedes resolviera’l problema usando una balanza como la de la figura 7, colgando nun estremu la corona y nel otru estremu un bloque d’oru puro del mesmu pesu que la corona. Nel aire la balanza taría equilibrada porque’l pesu la corona (P1) y el pesu’l bloque d’oru (P2) seríen iguales. Como yá diximos, si l’orfebre hubiere cambiao parte del oru por otru metal, la corona ocuparía más volume que’l bloque y entós l’empuxamientu (E1) que tira p’arriba de la corona sería mayor que’l del bloque d’oru (E2). La balanza desequilibraríase xubiendo la corona y baxando’l bloque.

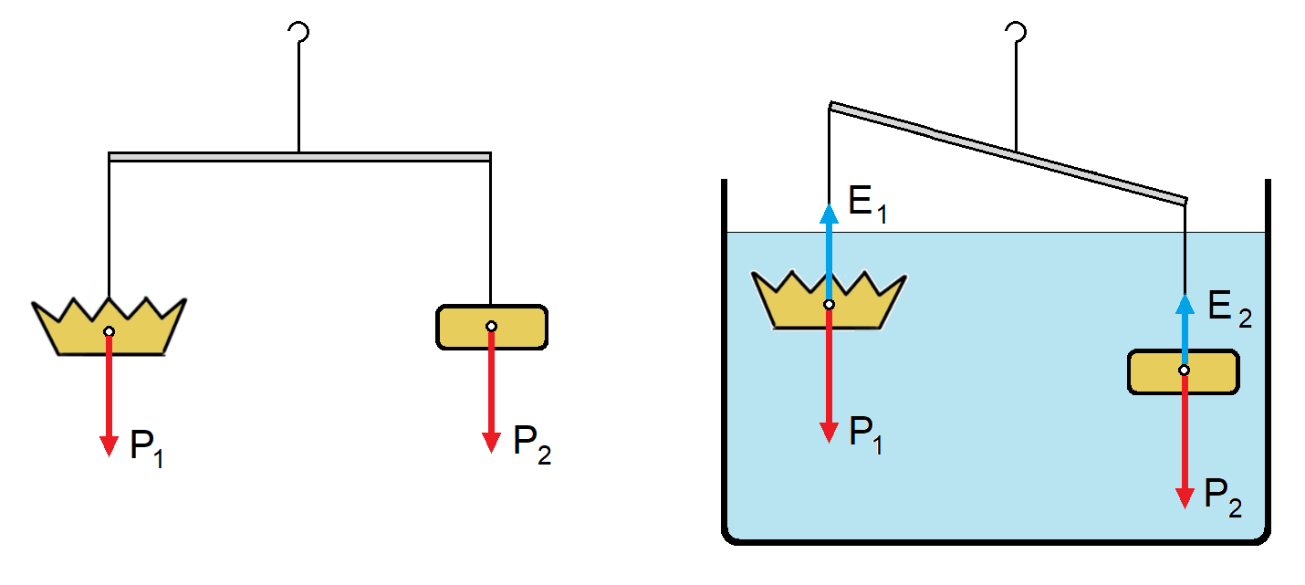
Figura 7. Una posible solución al problema de la corona

Si l’orfebre obró bien o mal nun ye cosa que se sepa a ciencia cierta, porque nun hai documentos que lo certifiquen, pero ye ésta una historia mui prestosa pa somorguiase (nunca meyor dicho) nesa ciencia qu’estudia’l comportamientu de los líquidos en reposu: la Hidrostática.